机器学习

CART_DBDT_Xgboost

从决策树到xgboost

ERAF post this 10496 words blog on September 24, 2018

找机会还是吧xgboost来好好总结一下！！

好吧 其实就是今天，之前对于boost的思想和bagging的思想其实都有所了解，这里直接复制粘贴一波 集成学习的三种思想 然后好好的总结一波其中的boosting 从adaboost到GBDT再到xgboost「其中顺带还会提到回归树」

集成学习

  • 基本思想：由多个学习器组合成一个性能更好的学习器「结合几个模型降低泛化误差」
  • 集成学习为什么有效？——不同的模型通常会在测试集上产生不同的误差。平均上，集成模型能至少与其任一成员表现一致；并且如果成员的误差是独立的，集成模型将显著地比其成员表现更好。「在花书上的P158页上 有关集成预测器的平方误差的计算也能看出来 当模型越不相关 导致着集成平方误差越小」

集成学习的基本策略(3)

关于集成学习算法的分类，一般是基于个体学习器之间的依赖关系，若有着强依赖关系、必须串连生成的序列化方法，一般指boosting方法；而不存在强依赖关系，可以同时生成的并行化方法，有bagging和随机森林等；

Bagging

  • Bagging 基于并行策略：基学习器之间不存在依赖关系，可同时生成。

  • 基本思路*：

    • 利用自助采样法对训练集随机采样，重复进行 T 次;

    • 基于每个采样集训练一个基学习器，并得到 T 个基学习器；

    • 预测时，集体投票决策**。

      自助采样法：对 m 个样本的训练集，有放回的采样 m 次；此时，样本在 m 次采样中始终没被采样的概率约为 0.368，即每次自助采样只能采样到全部样本的 63% 左右。 $lim_{m\rightarrow \infty}(1-\frac{1}{m})^m \rightarrow \frac{1}{e} \text{大致等于}0.368$

  • 特点：

    • 训练每个基学习器时只使用一部分样本 「看到上面先进行采样 再训练」
    • 偏好于不稳定的学习器作为基学习器； 「也就是针对那些对于样本分布较为敏感的学习器」

  • 代表算法/模型：

    • 随机森林：西瓜书P179
    • 神经网络的 Dropout 策略 花书P159

stacking

和下面所说的boosting类似，都是基于串行策略，：初级学习器与次级学习器之间存在依赖关系，初学习器的输出作为次级学习器的输入。

基本思路：

  • 先从初始训练集训练 T 个不同的初级学习器;
  • 利用每个初级学习器的输出构建一个次级数据集，该数据集依然使用初始数据集的标签；
  • 根据新的数据集训练次级学习器；
  • 多级学习器的构建过程类似。

周志华-《机器学习》中没有将 Stacking 方法当作一种集成策略，而是作为一种结合策略，比如加权平均和投票都属于结合策略。

为了降低过拟合的风险，一般会利用交叉验证的方法使不同的初级学习器在不完全相同的子集上训练

  以 k-折交叉验证为例：
  - 初始训练集 D={(x_i, y_i)} 被划分成 D1, D2, .., Dk；
  - 记 h_t 表示第 t 个学习器，并在除 Dj 外的数据上训练；
  - 当 h_t 训练完毕后，有 z_it = h_t(x_i)；
  - T 个初级学习器在 x_i 上共产生 T 个输出；
  - 这 T 个输出共同构成第 i 个次级训练数据 z_i = (z_i1, z_i2, ..., z_iT)，标签依然为 y_i；
  - 在 T 个初级学习器都训练完毕后，得到次级训练集 D'={(z_i, y_i)}

Boosting

  • Boosting（提升）方法从某个基学习器出发「使用的是初始训练集」，反复学习「根据基学习器的表现对训练样本进行调整」，得到一系列基学习器「达到一定的数目」，然后组合它们「如加权求和」构成一个强学习器。

    这里的基学习器 一般也常用于弱学习器 也就是那些泛化性能只是略好于随机猜测的学习器；「所以说集成学习也是一种用于提高泛化性能的方法啊」

  • Boosting 基于串行策略：基学习器之间存在依赖关系，新的学习器需要依据旧的学习器生成。

  • 代表算法/模型：
    • 提升方法 AdaBoost
    • 提升树
    • 梯度提升树 GBDT
  • Boosting 策略要解决的两个基本问题
    1. 每一轮如何改变数据的权值或概率分布？「如何调整训练数据」
    2. 如何将弱分类器组合成一个强分类器？「如何将训练好的弱分类器进行结合」

如上是来自算法/NLP/深度学习/机器学习面试笔记中对于boosting的总结，综上看看可以知道集成学习的三种方法的区别，从上面的介绍可以知道，boost方法就是每一步预测出来一个弱模型特征，然后累计加权到整体的模型之中，然后每次生成新模型的方法都是沿着损失函数的负梯度方向，进而达到逼近损失函数局部最小值的目的；「比如adaboost里面使用预测错误的数据集来训练新的模型 不就是为了降低错误率也就是损失函数吗」

boosting的公式推导 或者说是前向分布算法

进而 我们用公式来表达 因为知道使用boost方法的肯定是一个加法模型 也就是说它是由若干个基函数及其权值乘积之和的累加 ，因而我们有：$f(x)=\sum_{m=1}^{M}\beta_mb(x;\gamma_m)$ 明显的一个所占权重一个是基函数，那么在给定损失函数$L(y_i,\hat{y})$ 的情况下，学习得到这个加法模型就是个结构经验最小化 也就是损失函数期望最小化的问题有：

当然 一次性直接优化得到最终的模型不太现实，故前向分布算法就是从前到后 每一步之学习到一个基函数及其系数 逐步逼近损失函数的最小值，也就是说 我们每一步只要在上一步的基础上有所提升，求取其中一个基函数和其系数就好，因而就有：

若想让损失函数下降速度最快，那么下意识就想到了梯度下降：使新加的这一项刚好等于损失函数的负梯度，这样不就一步一步使得损失函数最快下降了吗？ 于是有：

其中λ可以和beta合并表示步长，那么对于这个基函数而言，其实它就是关于x和这个函数梯度的一个拟合，然后步长的选择可以根据线性搜索法，即寻找在这个梯度上下降到最小值的那个步长，这样可以尽快逼近损失函数的最小值。

对于GBDT，顾名思义，其中的基函数就是决策树，损失函数根据实际需要进行设计，但不变的还是使用梯度下降；这里我们首先还是先回顾一下回归树或者说决策树的东西吧；

回归树 - CART 决策树

  • CART 算法是在给定输入随机变量 X 条件下输出随机变量 Y 的条件概率分布的学习方法。

  • CART 算法假设决策树是二叉树，内部节点特征的取值为“是”和“否”。

    这样的决策树等价于递归地二分每个特征，将输入空间/特征空间划分为有限个单元，然后在这些单元上确定在输入给定的条件下输出的条件概率分布。

  • CART 决策树既可以用于分类，也可以用于回归；

    对回归树 CART 算法用平方误差最小化准则来选择特征，对分类树用基尼指数最小化准则选择特征

    基尼指数：对于有k个类来说，样本点属于第k类的可能性为p_k，那么概率分布的基尼指数就是$Gini(p)=\sum_{k=1}^Kp_k(1-p_k)$

CART 回归树算法推导

  • 一个回归树对应着输入空间/特征空间的一个划分以及在划分单元上的输出值； 「划分完成后的输出」

  • 若现有输入空间已经被分为M 个单元：{R_1,..,R_m,..,R_M}，并在每个单元上对应有输出值 c_m，则该回归树可表示为 ：$f(x)=\sum_{m=1}^Mc_mI(x\in R_m)$

    这里的I(x) 为指示函数 也就是是不是存在的意思「准确的说就是在所在区域才会为1 其他为0」

  • 如果已经划分好了输入空间，通常使用平方误差作为损失函数来表示回归树对于训练数据的预测误差，通过最小化损失函数来求解每个划分单元的最优输出值。

  • 进一步的，因为使用的平方误差，可以知道单元$R_m$上的输出$c_m$的最优输出值$\hat{c}m$ 为$R_m$上所有输入实例$x_i$ 对应的输出$y_i$的均值；

如何划分输入空间

可以看到 最优输出值 的表达式已经确定了，但问题还是在于 ：如何划分输入空间，不然无法划分出来对应的M个单元，依旧无法确定；

  • 一个启发式方法是：以特征向量中的某一个特征为标准进行切分。

    假设选择特征向量中第 j 个变量作为切分变量，然后选择某个实例中第 j 个值 s 作为切分点，则定义如下两个划分单元 「这里的 j 代表的还是假设，意思是遍历的意思，如果写成代码的话 就是先对 所有特征向量for i in feature_vector: 再进行一波对于当前的i特征向量 进行 for j in all_s_vector 每一个特征向量对应的一种切分点s 总还是能确定两个划分单元」

    也就是说：

    1.对于特征向量中第i个向量作为切分向量，选定某个实例中的第j个值s作为切分点有：

    2.遍历每个实例中可能的s值，在上面已经确定i向量作为切分向量的情况下，计算公式可以得到对于当前i向量最优的s值「选择最小的那个就好」：

    其中输出值 c1 和 c2 「划分的两部分各自的均值」分别为 ：

    3.遍历全部的特征变量 同样的操作1,2 找到最优的切分向量j 「也就是同样操作1,2后 得到全部上各自的那个平方误差 比较选取最小」构成(j,s) ，完成一次对于特征空间或者说输入空间的划分

    4.继续对两个子空间重复以上步骤，直到满足条件为止；得到将输入空间划分为M个区域的决策树

    $f(x)=\sum_{m=1}^Mc_mI(x\in R_m)$

    下面是一个完整示例：

    「因为仅有一个特征 于是不包括之后对于特征向量的遍历」

如上是对于CART的介绍，在此基础上 联动boosting，就出现了提升树的方法，和上面的CART基于训练数据 进行学习决策树「选特征i和其对应的j 进行划分空间 得到对应c 建立决策树 」不同的是，这里所采取的变成了残差，也就是真实的label值和其上一步间里的决策树的差值$r_{mi}=y_i-f_{m-1}(x_i)$ 进而基于这个残差 我们可用建立新的树「基于各个数据的残差 同样的参考上面选取特征和对应的值j 找到那个基于残差的划分点s，然后基于新的划分点 得到新的树 对整体更新」 算法描述如下

：

我们可以看到 这里所采用的使用残差来作为下一棵树的参照 进行学习下一个回归树，但如果我们把残差转化为上面提到的负梯度，进而我们可以得到关于GBDT的 描述：

也就是：进行到第m步的时候，基于损失函数和上一步的输出计算负梯度「前面的的残差其实就是一种在平方误差的时候的特例」

有了这个针对每个训练数据的负梯度后，我们可以使用$(x_i,r_{im})$ 这样一组数据，拟合出来第m个基函数。基于这个基函数可以将空间分为j个空间 ，而每个空间的输出 「也就是让损失函数最小的那个函数值」「就像之前选用均方误差作为损失函数，每次直接选取新划分区域的平均值作为c 其实也还是损失函数最小化的那个输出」就作为新的基函数的表达式有：

然后再和之前的函数合并，得到第m步的目标函数；

同样的思想 我们可用拿来看待adaboost「用于分类」，只是这里的损失函数被确定成为了一个指数损失函数$L(y,f(x))=exp(-yf(x))$ 意思就是当预测值确定的时候 两者相同 相乘就是为正 损失函数小，反之不相同 为负 损失函数就大，进而第m步的损失函数为

现在就是分别求α和G（x）使得损失函数最小值，前面那些部分$exp(-y_if_{m-1}(x_i))$ 不包含α和G(x)不用考虑，只要让后面那部分最小化就好；那么对于任意α大于0，希望$exp(-y_i\alphaG(x))$ 最小，只需要G(x)对于y的预测正确率最高即可「统计学习书上的最小化预测错误率也是一样」；

进而对于α的求解，就很直白的直接对于上面的损失函数进行对α求偏导就好，挺长的一串 难倒是不难 但是敲LaTeX太费事了 只给出一个最终的结果吧

这里的$e_m$ 代指的分类误差，参看统计学习中有着完整的推导；

从CATR到Boosting Tree再到GBDT

好 截止到现在 来让我们屡一下之前说过的东西；「离不开的都是基于CATR默认」

首先是这一类问题的基础CATR：基本公式是$f(x)=\sum_{m=1}^Mc_mI(x\in R_m)$，那么我们要做的就是划分出来适合的特征空间，得到M 个单元：{R_1,..,R_m,..,R_M}，并在每个单元上对应有输出值 c_m，构成这个回归树，因而问题就变成了：如何划分这M个单元。CART选用的是基于最优特征值来划分二分类，如果用公式来表达的话就是

具体的来说 就是每次 基于训练数据中的某类特征j和该特征某个值s来选取那个能让上面公式最小的值，同时划分出来的这两个类的输出值 c1 和 c2 就是划分的两部分各自的均值，原因是对于损失函数为平方误差的时候，能让其最小的时候 也就是取$y_i$均值的时候。基于此 我们完成一次对于数据的划分，以此类推 直到满足条件「损失函数的值降低到一定阈值」为止；得到将输入空间划分为M个区域的决策树 ；

紧接着在CART的基础上，联动着boosting的思想「多个基学习器的加权求和得到结果」 就得到了Boosting Tree，如果说BT和之前CART最大的不同 那么除了BT需要基于多个CART的累加之外，对于每个CART因为需要新学习器基于旧学习器进行学习和更新，从而下一步新的学习器基于当前模型的残差进行更新学习。

具体来说就是，当生成第m个决策树的时候，首先 我们需要产生一组基于当前模型和y_i的残差r_{mi} 即r_{mi}=y_i-f_{m-1}(x_i) ，「这里的f_{m-1}(x_i)代表的是之前m-1个决策树的加权累计」然后 现在的r_{mi}就替代了之前的训练数据成为了新的拟合数据，和上面CART同样的操作「毕竟基本训练器还是CART」：产生一棵完整的树，具体来说每一步： 对于现在训练数据中的某类特征j和该特征某个值s来选取那个能让CART公式最小的值，同时划分出来的表示两个类的输出值 c1 和 c2 就是划分的两部分各自的均值。进而 我们获得第m个决策树所划分的j个区域，得到对应区域表达的值：c_{mj}，进而得到第m棵树的表达式T_m=\sum c_{mj}I(x\inR_{mj}) ,进而我们还需要把这个树T_m和之前的模型进行合并 才能得到现在第m个的模型f_m=f_{m-1}+T_m ;

最后在说GBDT 要知道 上面的BT选用残差作为新的拟合数据的原因是其损失函数是平方误差，那么如果更为一般性的来说，残差其实就是均方误差的负梯度，所以 在GBDT里面，当我们产生第m个决策树的时候，我们产生的不再是残差 而是损失函数和当前模型f_{m-1}的负梯度，有

产生这样一组负梯度作为新的拟合数据，接着是和CART类似的操作 对于现在训练数据中的某类特征j和该特征某个值s来选取那个能让CART公式最小的值，但现在划分出来的表示两个类的输出值 c1 和 c2 不再是划分的两部分各自的均值，而是在各自新区域能让损失函数最小的函数值「毕竟均值也不过是对于均方误差里面能让其最小的存在」，以此类推，获得第m棵树划分的R_{mj}个区域，得到对应区域代表的值，于是我们得到第m个树T_m ,然后和之前的模型进行合并 才能得到现在第m个的模型f_m=f_{m-1}+T_m ;

Xgboost

有了现在这些的积累，可以去看现在这个炙手可热的基于树模型的XGBoost，其能很好地处理表格数据，同时还拥有一些深度神经网络所没有的特性（如：模型的可解释性、输入数据的不变性、更易于调参等）；

前面说这么多，主要还是为了打基础，说这里的xgboost，因为xgboost更多的还是在GBDT的基础上的改进；

###改变一：损失函数的正则项

首先是目标函数的改进：加入了正则项 ，毕竟GBDT的一大问题就是容易出现过拟合的问题，这里加入一个 和树的叶子结点数量T和叶节点的值「划分的区间的输出 就是那个c」有关的 正则项，

这里的$\omega$ 代表的是节点的权值「emmm 果然公式不统一看起来贼累」，毕竟对于决策树来说 最重要的就是一共有多少个节点以及每个节点的权值，所以决策树可以表示为

加入了这个正则项极好的限制了叶节点的数目，同时后面那个$w^2$的项 还起到了不让节点数值更极端的作用，可以理解做（某个样本label数值为4，那么第一个回归树预测3，第二个预测为1；另外一组回归树，一个预测2，一个预测2，那么倾向后一种，为什么呢？前一种情况，第一棵树学的太多，太接近4，也就意味着有较大的过拟合的风险 ）

总之考虑到原有的损失函数，现有的损失函数为$L(\phi)=\sum_{i}l(\hat y_i-y_i)+\sum_{k}[\gamma T+{1\over 2}\lambda   w   ^2]$ 起到了要求预测误差尽量小，叶子节点尽量少，节点数值尽量不极端的作用；

改变二：使用了二阶导数来优化

在BT或者GBDT里面，本质上 都是基于损失函数对于$f_{m-1}$的一阶导数构造的残差或者说负梯度，进行学习新的树 得到$f_m$ 。而xgboost不仅使用到了一阶导数，还使用二阶导数。 比如第t次的损失函数为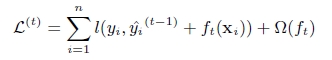： 对其做二阶泰勒展开：g代表一阶导数 h代指二阶导数 于是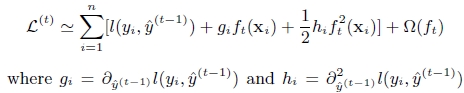

进而之后的推导，省略了常数项 将f(x)写回定义式，于是有:

第二步是因为不管fm如何取值第一项的值都不变，所以优化过程中可以不用考虑，第三步是因为对于每个样本而言其预测值就是对应输入空间对应的权值，第四步则是把样本按照划分区域重新组合，然后定义

代入后 对w求偏导使其为0，得到$w_j=-\frac{G_j}{H_j+\lambda}$ ;带回元式 消去w，进而得到了新的式子，

现在的损失函数变成只和上一步有关的新的损失函数，这也正是马上要说的第三点改变：分割点的改变，借由这个式子构建出来全新的切割点的选择方法，而不再是之前从CART到GBDT一脉相承的最小化均方误差。

改变三：最佳分割点的选取

从上面的描述我们知道 从CART到GBDT一脉相承，对于每次对于最佳分割点的选取 一直都是基于CART回归树那样 就基于最小化均方误差来选取最优分割点的「因为gbdt的弱分类器默认选择的是CART TREE。其实也可以选择其他弱分类器的，选择的前提是低方差和高偏差。框架服从boosting 框架即可。」 就是常说的

区别只是在于 其中的c计算方法的不同，当然本质上都是为了让损失函数最小化的目的；

在xgboost中，对于最佳切割点的选取标准是最大化得分公式来选取最优切割点的，可以看到 这里的g和h就是上面说的一阶导和二阶导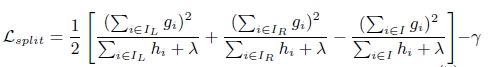

其中的四项 分别是：左叶的分数 右叶的分数 中间叶的分数，给主叶的正则项；这同时也起到了“剪枝”的作用——如果分数小于γ，则不会增加分支；

其他关于xgboost的修改优化

xgboost算法的步骤和GB基本相同，都是首先初始化为一个常数，gb是根据一阶导数ri，xgboost是根据一阶导数gi和二阶导数hi，迭代生成基学习器，相加更新学习器。

除了上面三点之外，其他xgboost还有一定的改进，比如：

  • 在寻找最佳分割点时，传统的方法会枚举每个特征的所有可能切分点。XGBoost 实现了一种近似的算法，大致的思想是根据百分位法列举几个可能成为分割点的候选者，然后从候选者中根据上面求分割点的公式计算找出最佳的分割点。
  • XGBoost 考虑了训练数据为稀疏值的情况，可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率，paper 提到能提高 50 倍。
  • 特征列排序后以块的形式存储在内存中，在迭代中可以重复使用；虽然 Boosting 算法迭代必须串行，但是在处理每个特征列时可以做到并行。
  • 按照特征列方式存储能优化寻找最佳的分割点，但是当以行计算梯度数据时会导致内存的不连续访问，严重时会导致 cache miss，降低算法效率。Paper 中提到，可先将数据收集到线程内部的 buffer，然后再计算，提高算法的效率。
  • XGBoost 还考虑了数据量比较大的情况，当内存不够时怎么有效的使用磁盘，主要是结合多线程、数据压缩、分片的方法，尽可能的提高算法的效率。

关于决策树 GDBT Adaboost、xgboost的实战对比

好吧，这里还是直白的掉包侠登场的时候了「知道自己代码写的有多烂的（扭头）」；

采用的sklearn里面那个经典的鸢尾花数据库，选用前2个特征进行训练，比较在训练集和测试集上的表现：

import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import datasets
import xgboost as xgb
 
iris=datasets.load_iris()
x=iris.data[:,:2]
y=iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.7, random_state=1)

model1=DecisionTreeClassifier(max_depth=5)
model2=GradientBoostingClassifier(n_estimators=100)
model3=AdaBoostClassifier(model1,n_estimators=100)

data_train = xgb.DMatrix(x_train,label=y_train)
data_test=xgb.DMatrix(x_test,label=y_test)
param = {}
param['objective'] = 'multi:softmax'
param['eta'] = 0.5
param['max_depth'] = 8
param['silent'] = 1
param['nthread'] = 4
param['num_class'] = 3
watchlist = [ (data_train,'train'), (data_test, 'test') ]
num_round = 10
bst = xgb.train(param, data_train, num_round, watchlist );
pred = bst.predict( data_test );


model1.fit(x_train,y_train)
model2.fit(x_train,y_train)
model3.fit(x_train,y_train)
model1_pre=model1.predict(x_train)
model2_pre=model2.predict(x_train)
model3_pre=model3.predict(x_train)
res1=model1_pre==y_train
res2=model2_pre==y_train
res3=model3_pre==y_train
model1_pre_test=model1.predict(x_test)
model2_pre_test=model2.predict(x_test)
model3_pre_test=model3.predict(x_test)
res1_test=model1_pre_test==y_test
res2_test=model2_pre_test==y_test
res3_test=model3_pre_test==y_test
print ('决策树训练集正确率%.2f%%'%np.mean(res1*100))
print ('GDBT训练集正确率%.2f%%'%np.mean(res2*100))
print ('AdaBoost训练集正确率%.2f%%'%np.mean(res3*100))
print ('决策树测试集正确率%.2f%%'%np.mean(res1_test*100))
print ('GDBT测试集正确率%.2f%%'%np.mean(res2_test*100))
print ('AdaBoost测试集正确率%.2f%%'%np.mean(res3_test*100))

res4=bst.predict( data_train )==y_train
res4_test=bst.predict(data_test)==y_test
print ('xgboost训练集正确率%.2f%%'%np.mean(res4*100))
print ('xgboost测试集正确率%.2f%%'%np.mean(res4_test*100))

决策树训练集正确率84.76%
GDBT训练集正确率95.24%
AdaBoost训练集正确率95.24%
决策树测试集正确率75.56%
GDBT测试集正确率62.22%
AdaBoost测试集正确率62.22%
xgboost训练集正确率94.29%
xgboost测试集正确率66.67%

emmmmm 效果就先不说了…这几个算法也是第一次用 调参看看结果会更好吧，可以看到几种boosting的方法表现比单纯的仅仅是要好，至于测试集上的样子 emmmm 果然还是过拟合了；

这里主要说一下关于xgboost的一些设置：

  • objective：设置的是你的分类的目标及方法，除了我们用的多分类的multi:softmax，还可以是binary:logistic，reg:logistic等等，根据你的目标需要去设置。
  • eta：设置的是衰减因子，就是在步长前面乘以一个系数，设置过小容易导致计算时间太长，太大又很容易过拟合；
  • max_depth：是所用的树的最大深度；
  • silent：打印运行信息；
  • num_class：类别数，与 multisoftmax 并用
  • nthread：调用的线程数
  • num_round：迭代计算次数；
  • lambda：控制模型复杂度的权重值的L2正则化项参数，参数越大，模型越不容易过拟合。
  • colsample_bytree ：生成树时进行的列采样

更具体的可以在官方文档中看到;

CATALOG
    FEATURED TAGS
    强化学习 生活 深度学习 autonomous driving 机器学习 碎碎念