深度学习

DL之优化方法

对于GD的两类改良

ERAF post this 6025 words blog on October 7, 2018

前言

忽然感觉这应该弄成一个专题，毕竟深度学习的那些 从流程也能看出来 几个需要重点思考的：网络结构：「其中还涉及了 激活函数 的选取 层宽度 层深度 核大小等一系列问题」，构建好结构后 什么样的参数是需要的 就涉及了 损失函数的构建，如何朝着这样一个需要的参数前进 就涉及 优化方法的选取，本文主要涉及对于优化方法的选取，后面会谈到激活函数的选取，至于损失函数 会在本文最后一笔带过 毕竟大多就是那几类及变形；

学习和优化的区别

在文章之前 首先涉及一个概念就是：学习和优化的区别。其实这里的标题说的是：优化，并不是很恰当的，毕竟深度学习对于损失函数的优化最小化，最终目的不还是为了得到一个优秀的参数吗？进而说 学习和优化的区别主要在于，优化是途径，通过这一个途径进而使我们希望某些性能度量来达到满足条件「优化损失函数 得到一个满意的准确率」；

梯度下降

首先，梯度下降是一种优化算法，其通过迭代的方式寻找到模型的最优参数；这里所说的最优参数意思是目标函数达到最小值时候的解；

忽然想起之前见到的一个问题「神经网络引入激活函数放弃凸性的意义」，这里提到的凸性就是放弃目标函数作为凸函数，如果是凸函数的时候 梯度下降达到局部最小值的时候 就一定是全局最优解，但非凸函数，如神经网络就会存在多个局部最优解，所以一般情况下，梯度下降无法保证全局最优。

而梯度下降法，顾名思义是采用负梯度方向作为损失函数下降最快的指导，包含的意义在于：微积分中 基于梯度方向是函数增长最快的方向；更细致地说 所谓梯度是损失函数针对于各个参数的偏导的向量；

  • 梯度仅仅指示了对于每个参数各自增长最快的方向；因此，梯度无法保证全局方向就是函数为了达到最小值应该前进的方向。
  • 梯度的具体计算方法即反向传播。

负梯度包含的信息：正负号代指了当前参数应该调大或者降低「正大 负小」；每一项的绝对值 代指了每个参数对于函数达到最值的影响程度；

随机梯度下降

在梯度下降的基础上，产生了两种新的梯度下降法；

首先 传统的梯度下降每次都是用全部的训练样本进行计算平均偏差，进而基于这种平均偏差来更新参数；这就带来了一个问题就是：每次对模型参数进行训练的时候 都需要对于全部的数据进行遍历，这样当样本数据量很大的时候 就很不现实；

因而引入随机梯度下降的方法，每次使用单个样本的损失来近似表达平均损失，这也就是所谓在线学习了；

小批量随机梯度下降

但 每次只使用的单个训练样本代表整体进行训练，也会带来方差较大的问题，于是为了降低随机梯度的方差，使模型迭代更加稳定，实践中会使用一批随机数据的损失来近似平均损失。 「借助批训练方法，可以借助并行计算的方法来加快运算」

小批量随机梯度下降的训练过程：

  1. 在训练集上抽取指定大小（batch_size）的一批数据 {(x,y)}

  2. 【前向传播】将这批数据送入网络，得到这批数据的预测值 y_pred

  3. 计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离

  4. 【反向传播】计算损失相对于所有网络中可训练参数的梯度 g

  5. 将参数沿着负梯度的方向移动，即 W -= lr * g

    lr表示学习率

这里提到了批梯度下降 那么就带来了一个问题就是：

批 的大小对于优化效果的影响

  • 较大的批能得到更精确的梯度估计，但回报是小于线性的，也就是说 不代表批越大就表现一定越好。

  • 较小的批能带来更好的泛化误差，泛化误差通常在批大小为 1 时最好。

    原因可能是因为小批量在学习过程中会引入噪声，使其产生了一定的正则化的效果；

    但 小批量的梯度下降也会带来更大的方差，于是会选用更小的学习率 来保证稳定性，但也意味着更长的训练时间；

  • 同时批的设置 选用为2的幂数的时候能够充分利用矩阵运算操作，所以批的大小一般取 32、64、128、256 等。

随机梯度下降存在的问题

  1. 相比于原始的梯度下降，随机梯度下降或者批梯度下降都是放弃梯度计算的准确性，也就是说 只用一部分样本计算的结果就代指了整体，因而SGD对于梯度的估计往往可能不那么准确，可能会导致目标梯度收敛不稳定 或者不收敛l；
  2. 同时 无论是传统的梯度下降还是随机梯度下降都可能遇到局部极值的问题。
  3. SGD可能遇到“峡谷”和“鞍点”两种情况

关于“峡谷”和“鞍点”两种情况 的定义：

  • 峡谷类似一个带有坡度的狭长小道，左右两侧是“峭壁”；在峡谷中，准确的梯度方向应该沿着坡的方向向下，但粗糙的梯度估计使其稍有偏离就撞向两侧的峭壁，然后在两个峭壁间来回震荡。「一个带有坡度的小道，正常的移动方向应该是沿着小道直接向下，但因为梯度计算的问题 没有计算得到正确的梯度方向于是就在坡道内部左右徘徊的下降」「梯度下降计算的问题」
  • 鞍点的形状类似一个马鞍，一个方向两头翘，一个方向两头垂，而中间区域近似平地；一旦优化的过程中不慎落入鞍点，优化很可能就会停滞下来。「固定的学习率 导致只能在原地徘徊 找不到下降的地方」

对于随机梯度下降的改进

大致分为两个类：惯性保持和环境感知

惯性保持指的是加入动量 SGD 算法；

环境感知指的是根据不同参数的一些经验性判断，自适应地确定每个参数的学习速率 ，比如adam

带有动量的SGD（momentum方法）「SGD改进方向的惯性保持」

带有动量的momentum方法有两方面的好处：一方面是可以解决“峡谷”和“鞍点”问题；一方面也可以用于SGD 加速，特别是针对高曲率、小幅但是方向一致的梯度。 「解决峡谷和鞍点的问题，梯度下降加速」

更新公式中 引入了变量v作为速度，α代指的是动量参数，学习率变成了ε，进而现在有：

这里的g依旧是计算得到的梯度，但借助引入的动量参数$\alpha$，构建出来新的用于更新参数的变量v，可以看到v是个随着g的值不断更新的值：$V \leftarrow \alpha V-\epsilon g$ 当g一直相同的时候，也就会导致在-g方向不断加速，直到最大的$V \leftarrow \frac{-\epsilon g}{1-\alpha}$ ;「毕竟上面的更新公式 当g相同的时候 不就是公比为α等比数列吗」于是

  • 在实践中， α 的一般取 0.5, 0.9, 0.99，分别对应最大 2 倍、10 倍、100 倍的步长
  • 和学习率一样α 也可以使用某种策略在训练时进行自适应调整；一般初始值是一个较小的值，随后会慢慢变大。

再直观的理解一下momentum的SGD：

  • 如果把原始的 SGD 想象成一个纸团在重力作用向下滚动，由于质量小受到山壁弹力的干扰大，导致来回震荡；或者在鞍点处因为质量小速度很快减为 0，导致无法离开这块平地。
  • 动量方法相当于把纸团换成了铁球；不容易受到外力的干扰，轨迹更加稳定；同时因为在鞍点处因为惯性的作用，更有可能离开平地。
  • 动量方法以一种廉价的方式模拟了二阶梯度（牛顿法）

「其实就还是当计算得到的梯度类似的时候 会加大梯度下降的程度」

NAG 算法（Nesterov 动量）（momentum方法）「SGD改进方向的惯性保持」

NAG的方法参考算法实现也知道，在计算梯度之前又加上了一个对于参数施加V的操作；「多进行一次临时更新来计算得到一个修正因子」直白的理解成 朝着标准动量方法里面添加了一个修正因子。

AdaGrad （自适应学习率）「环境感知」

可以联系花书上的P187进行看；

对于AdaGrad来说，简单的说就是独立的适应模型中的每个参数：具有较大偏导值就对应的设置一个大的学习率，如果是小的偏导值就对应的设置一个小的学习率，具体来说就是：

每个参数的学习率会缩放各参数反比于历史梯度平方值总和的平方根，也就是说每次更新的时候 学习率ε需要处理历史梯度平方的总和的平方根，反映到公式就是$\Delta\theta \leftarrow -\frac{\epsilon}{\delta+\sqrt{r}}$ 这里的r计算方式就是历史梯度的平方的和；算法描述如下：

可以看到 每次算法的学习率ε依旧是一个定值，只是每次每个参数进行使用的时候 考虑到之前的梯度情况进行得到一个新的学习率；

AdaGrad 存在的问题

  • 学习率是单调递减的，训练后期学习率过小会导致训练困难，甚至提前结束
  • 需要设置一个全局的初始学习率

RMSProp（自适应学习率）「环境感知」

可以看到Adagrad的方法，里面的学习率随着梯度的累加是不断减少的，所以也就会导致学习率过度衰减的问题；因而可能出现：当还没到达局部最小值之前就已经变得太小而无法训练了。

进而RMSProp的方法使用指数衰减平均「递归定义」的方法来丢弃遥远的历史，进而说 这里引入了一个新的参数ρ，而ρ就是向我们下面所说的β起着一样的作用，于是现在有着：

$r \leftarrow \rho . r+(1-\rho.g^2)$

$RMS[g]=\sqrt{r+\delta}$

$\Delta \theta=-\frac{\epsilon}{RMS[g]}.g$

指数衰减平均在之前deeplearning.ai的课程中说过，大致就是求均值的时候 不再是直接的相加除以个数，而是这样的公式$v_t=\beta v_{t-1}+(1-\beta)\theta_t$

可以看到各个数值的权重随着时间的增加 而发生指数式的衰减，越新的数据有着更大的加权 而较旧的数据也有着加权不过很小；

整体的算法描述如：

联系上面的NAG的带有Nesterov动量的RMSProp为：

可以看到和上面的RMSProp的方法区别就在于，在计算梯度g之前先进行了一次临时更新 计算得到一个修正因子来用于更新；

  • RMSProp 建议的初始值：全局学习率 ϵ=1e-3，衰减速率 ρ=0.9

  • 经验上，RMSProp 已被证明是一种有效且实用的深度神经网络优化算法。
  • RMSProp 依然需要设置一个全局学习率，同时又多了一个超参数（推荐了默认值）。

AdaDelta「RMSProp的变种」（自适应学习率）「环境感知」

AdaDelta和RMSProp都是为了解决AdaGrad学习率衰减的问题而诞生的。

两者前半部分大致相同 区别主要在于：学习率的计算的时候，AdaDelta不再需要设置一个初始学习率，只需要使用

这里的$RMS[]$操作来自于之前的RMSProp，其中有着$RMS[g]t=\sqrt{r_t+\delta}=\sqrt{\rho.r{t-1}+(1-\rho).g^2}$ ，那么同样的$RMS[\Delta \theta]{t-1}=\sqrt{\rho.r’{t-2}+(1-\rho).g^2}$ ;

Adam（自适应学习率）「环境感知」

相比于RMSProp来说，Adam除了原有的历史梯度平方的指数衰减r之外，又添加了历史梯度的指数衰减s,相当于动量

算法描述如：

可以看到 这里又多计算一个s，计算方式虽然都是指数衰减平均，但是使用的只是历史梯度；

同时可以发现 这里多出了两步偏差修正：原因是：

  • 注意到，s 和 r 需要初始化为 0；且 ρ1 和 ρ2 推荐的初始值都很接近 1（0.9 和 0.999）
  • 这将导致在训练初期 s 和 r 都很小（偏向于 0），从而训练缓慢。
  • 因此，Adam 通过修正偏差来抵消这个倾向。

AdaMax（自适应学习率）「环境感知」

  • Adam 的一个变种，对梯度平方的处理由指数衰减平均改为指数衰减求最大值

Nadam（自适应学习率）「环境感知」

  • Nesterov 动量版本的 Adam

如何选择这些优化算法？

  • 各自适应学习率的优化算法表现不分伯仲，没有哪个算法能在所有任务上脱颖而出；
  • 目前，最流行并且使用很高的优化算法包括 SGD、带动量的 SGD、RMSProp、带动量的 RMSProp、AdaDelta 和 Adam。
  • 具体使用哪个算法取决于使用者对算法的熟悉程度，以便调节超参数。

各优化算法的可视化

SGD 各优化方法在损失曲面上的表现

SGD 各优化方法在鞍点处上的表现

基于二阶梯度的算法

牛顿法

本质上算法实现参考花书P191，就是在计算梯度的基础上，又计算了一个海赛矩阵 也就是损失函数针对全部参数的一个二阶导组成的矩阵；基于计算的这个损失函数对于参数的二阶导组成矩阵 对其求逆矩阵，逆矩阵乘上梯度 就是得到的$\Delta \theta$ ,然后用于更新；

拟牛顿法就是用正定矩阵来近似Hessian矩阵的逆

  • 梯度下降使用的梯度信息实际上是一阶导数
  • 牛顿法除了一阶导数外，还会使用二阶导数的信息
  • 根据导数的定义，一阶导描述的是函数值的变化率，即斜率；二阶导描述的则是斜率的变化率，即曲线的弯曲程度——曲率

几何理解

  • 牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面；而梯度下降法是用一个平面去拟合当前的局部曲面。
  • 通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

牛顿法优缺点

优点

  • 收敛速度快，能用更少的迭代次数找到最优解

缺点

  • 每一步都需要求解目标函数的 Hessian 矩阵（海塞矩阵）的逆矩阵，计算复杂

    Hessian 矩阵即由二阶偏导数构成的方阵

为什么牛顿法比梯度下降收敛更快

常见的几种最优化方法（梯度下降法、牛顿法、拟牛顿法、共轭梯度法等） -

牛顿法实现

统计学习附录B

优化方法的对比

随机梯度下降（SGD）
缺点
选择合适的learning	rate比较难	
对于所有的参数使用同样的learning rate	
容易收敛到局部最优
可能困在saddle point
SGD+Momentum
优点：
积累动量，加速训练
局部极值附近震荡时，由于动量，跳出陷阱
梯度方向发生变化时，动量缓解动荡。
Nesterov Mementum
与Mementum类似，优点：
避免前进太快
提高灵敏度
AdaGrad
优点：
控制学习率，每一个分量有各自不同的学习率
适合稀疏数据
缺点
依赖一个全局学习率
学习率设置太大，其影响过于敏感
后期，调整学习率的分母积累的太大，导致学习率很低，提前结束训练。
RMSProp
优点：
解决了后期提前结束的问题。
缺点：
依然依赖全局学习率
Adam
Adagrad和RMSProp的合体
优点：
结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
为不同的参数计算不同的自适应学习率
也适用于大多非凸优化 -	适用于大数据集和高维空间
牛顿法
牛顿法在迭代的时候，需要计算Hessian矩阵，当维度较高的时候，计算 Hessian矩阵比较困难
拟牛顿法
拟牛顿法是为了改进牛顿法在迭代过程中，计算Hessian矩阵而提取的算法，它采用的方式是通过逼近Hessian的方式来进行求解。

常见损失函数

首先是损失函数是什么，这里需要涉及一个对于期望风险 期望风险 「针对整个模型」 表示的是全局的概念，表示的是决策函数对所有的样本<X,Y>预测能力的大小，而经验风险 「针对训练集」则是局部的概念，仅仅表示决策函数对训练数据集里样本的预测能力。

损失函数描述为结构经验 包括两部分：经验风险函数加上正则项

交叉熵损失函数「LR」 均方误差、0-1损失函数、绝对值损失函数、Adaboost里面的指数损失函数、SVM里面的Hinge损失函数「拉格朗日乘子式子的变形」；

然后是交叉熵损失函数：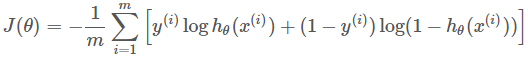

平方损失函数：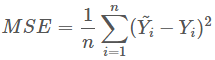

指数损失误差「adaboost」

Hinge损失函数「SVM」后面的项相当于L2正则项

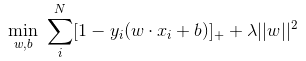
其他损失函数

CATALOG
    FEATURED TAGS
    强化学习 生活 深度学习 autonomous driving 机器学习 碎碎念