简单的来谈一下这段时间看RNN时候遇到的一点有关概念的理解方面的东西，基本上包含一些基础概念和tensorflow里面的东西；
RNN的多层和时序的概念
不知道有没有和我遇到一样的问题，在一开始看RNN的结构图
直白的把其中的$h_1$、$h_2$等结构看成了就是FCN里面的第一隐层 第二隐层这样的关系，进而导致到后面对于tensorflow其中前向传播的时候call方法和dynamic_rnn等方法理解的偏差：认为每次调用一次call方法完成的是一个单隐层的前向移动，进而理解后面构成多层的tf.nn.rnn_cell.MultiRNNCell时候，也就认为多层也需要多次调用call方法才能完成对于一次前向传播的进行，导致混乱；
实际上呢？当然不是这样啦，这里的图其实如果换成循环结构的图可能就更好理解一点；
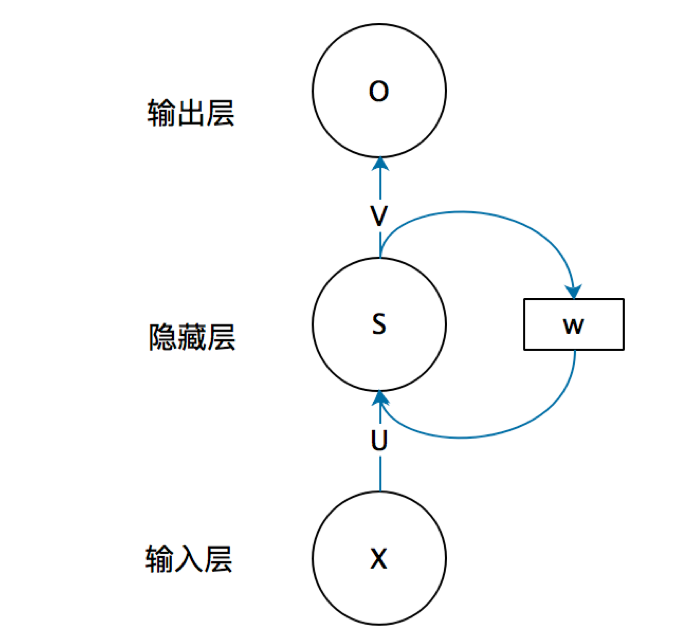这里其实也就是RNN里面多层和时序概念的区别，对于RNN里面其实涉及了时序推进这样的h_1、h_2...，同时又涉及多层这样的隐层1和隐层2，因而会感觉很困惑，但实际上还是很好理解的，两者相互依存；
说他们相互依存：首先RNN本身可以用于处理时序信息，也就是前后包含相关关系的输入数据，比如基于文本数据进行后面文字的预测，而这样的能力就是依托于上面的结构来实现的；而 只是单层单元可能无法处理包含更为复杂特征的数据，因而需要对于每个单元进行处理，进行网络层数的增加，来解决更为复杂的问题；这样说的也就是说的很直白了，上面所表示出来的结构中单元的个数表示了设置的时序信息的长度，反映到tf.nn.dynamic_rnn里面的话，可以是input里面的max_time，或者是本身的sequence_length参数，这里我们后面再说；
RNN里面的前向和反向传播
首先这里所说的前向和后向，要和常规的FCN分开，毕竟对于RNN来说其中的输出，根据如上图中展示的时序个数有关，同样的 损失函数反向传播的时候，首先要考虑的是损失来自的是哪个时序单元，再考虑在某个单元内部多层的反向传播。「可以观察一些示范代码中RNN损失函数的定义，其都会考虑到有关序列的累加」
因而这里所说的前向，说的其实也就是在时序中传递信息的前后关系，至于每个单元内部多层间的操作就和FCN是一样了。这里应该各种资料里面说的已经够多了，只是放一些自己的笔记，说一些自己的思路；
就像RNN最基本的概念和用处一样：解决序列数据的问题，这里的序列数据可能是时序也可能是其他，但不变的一点肯定是说：前后数据之间是有关系的，换句话说 某一时刻所做出决策或者映射结果不再是只是因为当前的输入得到的，而是还需要考虑之前的情况，因而这里我们引入一个新的变量来描述 之前状态情况和当前的输入 共同作用得到当前时刻下最终的输出；
因而 对于t时刻的输出，其实输入我们应该设置一个新的变量$h_{t-1}$用于描述之前时刻对于该时刻的影响。进而 考虑到当前时刻之后，现在的$h_t$应该是$h_t=f(Ux_t+Wh_{t-1}+b)$，在此基础上 在设置新的权值得到正常的输出$y_t=softmax(Vh_t+c)$, 前面的U和W等参数更多的还是相当于设置：当前时刻输入和之前状态情况所占的比重，这里的V等才是真正的用于建立映射；
前面的f我们一般使用tanh的激活函数来表示，完成对于参数的设置，进而在代码中的体现 比如tensorflow的源代码中的call方法。「毕竟本质上call方法不就是一种在时序上的前向吗」
def call(self, inputs, state):
"""Most basic RNN: output = new_state = act(W * input + U * state + B)."""
if self._linear is None:
self._linear = _Linear([inputs, state], self._num_units, True)
output = self._activation(self._linear([inputs, state]))
return output, output
如上是BasicRNNCell里面的call方法，可以看到这里本来应该输出output,state的，输出的两个其实都是一样的东西。当然这里还是为了简洁考虑，在实际代码中就需要对于output再加上tf.nn.softmax来完成对应操作了就；
基本的RNN内部操作就是这样，如果是LSTM的话，其实内部就又涉及包括遗忘门、记忆门、输出门等概念，这里我们后面再说；
然后对于其中的有关时序的RNN反向传播，显然的对于V和c，直接建立就好，但是如果设置U和W，那么就会涉及$h_t$ 先对于$h_t$进行求偏导倒是，显然对于其求偏导 包含两部分 一个是从$y_t$直接得到的，另外一个就是从$y_{t+1}$经过$h_{t+1}$得到的；如下：
首先要知道RNN的前向传播，有：$a^{(t)}=b+Wh^{(t-1)}+Ux^{(t)}$;$h^{(t)}=tanh(a^{(t)})$ ;$o^{(t)}=Vh^{(t)}+c$ ; $\hat{y}_t=softmax(o^{(t0})$
RNN中的损失函数来自于不同时间步的损失函数的累加，也就是$L=\sum_t L^{(t)}$ ;这样计算c和V的梯度还是比较简单的有：
$\frac{\partial L}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)}$
「emmm 就是这种如同DNN一样 直接链式法则的意思」
同理：$\frac{\partial L}{\partial V} =\sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial V} = \sum\limits_{t=1}^{\tau}(\hat{y}^{(t)} - y^{(t)}) (h^{(t)})^T$
但对于W,U,b 来说就很麻烦了，毕竟参考上面的前向传播的公式知道，其需要基于$h(t)$ 才能进行计算；因而需要$\frac{\partial L}{\partial h(t)} $,但是正常的有关h(t)的计算梯度应该包含两部分：当前位置的梯度损失和下一时刻的梯度损失，也就是说：反向传播时，在在某一序列位置t的梯度损失由当前位置的输出对应的梯度损失和序列索引位置 t+1时的梯度损失两部分共同决定。
于是我们得到$\delta^{(t)} =\frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}} $
$=\frac{\partial L}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial h^{(t)}} + \frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial a^{(t+1)}}\frac{\partial a^{(t+1)}}{\partial h^{(t)}}$
$= V^T(\hat{y}^{(t)} - y^{(t)}) + W^T\delta^{(t+1)}diag(1-(h^{(t+1)})^2)$
可以看到 前面一项是：基于当前项求取关于h(t)的梯度；后面一项就是：基于下一时刻h(t+1)来求取h(t)梯度；显然从h(t+1)到h(t)除了相关的权值之外，需要经过激活函数tanh；
##RNN和LSTM
首先 当然要知道的是为什么要有LSTM，或者说LSTM相比于基本的RNN结构有什么好处；
对于普通的RNN来说，其反向传播的计算 肯定包含对于每一部梯度的联乘，梯度爆炸和梯度消失的原因也都是来自于这，显然也就不适合处理时序较长的问题 无法处理「长期依赖」问题，也就无法学到序列中蕴含的间隔较长的规律，也就是说不能用于处理较长时间序列的问题，具体表现就像是对于一个句子的预测 可能只能基于当前单词之前两三个单词进行预测，而不能通篇的考虑整个句子。
这时候就出现了一个新的对于RNN的改进版：LSTM，其作为门控RNN的一种，和其他的对于RNN的改进方法一样 都可以用于长期的时序信息的记住 同时保证导数不消失而不会发生爆炸。但相比于其他的方法 一方面 每个时间步可以动态的设计连接权值，另一方面 其累积的时间尺度也可以动态的改变。「emmm 这一部分不是太理解 说的也不太全面 可以参考花书P248」
从名字来说 翻译过来就是长短期记忆网络；我们都知道 在RNN里面再计算隐函数的时候 有$h_t=f(Ux_t+Wh_{t-1}+b)$ 这里的f一般也就是代指着tanh激活函数，显然可以从中看到 主要考虑到之前的隐函数信息和当前时刻的外界输入信息，而LSTM在此基础上又增加了一些部分，除了都有的$h_t$之外又增加了$C_t$这个概念，因此每个隐函数输出就不只是有$h_t$ 还有着$C_t$,两者的图如下：
和
在后者的LSTM里面每个隐函数单元里面，水平线带智者这里引入的新参数：内部记忆状态$C_t$,显然从图中可知 其来历是来自于上一步的$C_{t-1}$ 但却不是照搬之前的$C_{t-1}$，因而这里引入了一个新的概念：遗忘门 用于控制遗忘掉$C_{t-1}$的哪些部分，如下图：
这里的$\sigma$ 也就是所说的sigmoid激活函数，引入其中的输入包含两部分：之前的隐函数和当前的输入。我们都知道sigmoid的作用有着可以将输入映射到0-1之间的作用，经过遗忘门的权值$W_f$和两种输入$[h_{t-1},x_t]$相乘 得到一个最终和$C_{t-1}$形状相同的矩阵，矩阵和$C_{t-1}$逐点相乘。显然$f_t=\sigma(W_f [h_{t-1},x_t]+b_f )$越接近0的就是越容易被遗忘的。「原有的状态情况」
只是遗忘肯定不行，还需要保证LSTM还能记住多少新东西，也就是记忆门 或者说输入门控制当前计算的新状态以多大的程度更新到记忆状态中：
从图中可用知道，其输入依旧是$x_t$和$h_{t-1}$，但输出包含两部分：一个是$i_t$和之前遗忘门里面的$f_t$一样经过sigmoid激活函数，另外一个是经过tanh激活函数的「虽然都类似 看起来只是激活函数的不同，但显然都有着不同的权值」，然后判断多大程度的该被记住的方式 也就是让$\tilde{C_t}$和$i_t$逐点相乘；「产生新的状态情况」
进而说当前“记忆状态 $C_t$”间的状态转移由输入门和遗忘门共同决定:
在完成对于内部状态$C_t$的确定之后，当前隐函数最终的输出，其实还涉及一个输出门的概念，输出门也就是在当前的内部状态$C_t$的基础上，对于其进行tanh激活函数，然后同样的使用sigmoid激活函数进行设置计算控制当前的输出有多大程度取决于当前的记忆状态
因而完整的LSTM公示如下：
call方法
首先call方法的用处，上面其实也提到了关于RNN里面多层和多时间步之间的关系，那么 在tensorflow中，建立多层很简单，而建立起来这种时间步之间的关系，也就是：「输入上一步的状态信息和当前的输入信息 进而计算当前步的输出和状态信息」，而建立这个一步 所使用的就是tf.nn.rnn_cell；
首先来说 rnn_cell作为抽象类并不能实例化，因而基于其子类的BasicRNNCell和BasicLSTMCell来使用，每个单元都有着需要设置的参数 比如其中的状态单元数目等。进一步的 肯定单层的无法有很好的效果，需要进行堆叠；显然RNN不再只是像CNN那样，前后只是输入输出的联系 直接头尾相连就好，这里需要一个引入一个函数MultiRNNCell来对于RNN进行堆叠，但注意这里的多层并非所说的多个时序的概念，而仅仅是一个时序单元中经过多个层而已「其中进行的就是第一层的状态输出作为第二层的输入 第二层的状态输出作为第三层的输入以此类推」如下：
def get_a_rnncell():
return tf.nn.rnn_cell.BasicLSTMCell(num_units=128)
model=tf.nn.rnn_cell.MultiRNNCell([get_a_rnncell() for _ in range(3)])
>>> model.state_size
(LSTMStateTuple(c=128, h=128), LSTMStateTuple(c=128, h=128), LSTMStateTuple(c=128, h=128))
#包含了三个隐状态情况
>>> h_0=model.zero_state(100,tf.float32)
>>> output,h1=model.call(input_data,h_0)
>>> h1
(LSTMStateTuple(c=<tf.Tensor 'cell_0/cell_0/basic_lstm_cell/add_1:0' shape=(100, 128) dtype=float32>, h=<tf.Tensor 'cell_0/cell_0/basic_lstm_cell/mul_2:0' shape=(100, 128) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'cell_1/cell_1/basic_lstm_cell/add_1:0' shape=(100, 128) dtype=float32>, h=<tf.Tensor 'cell_1/cell_1/basic_lstm_cell/mul_2:0' shape=(100, 128) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'cell_2/cell_2/basic_lstm_cell/add_1:0' shape=(100, 128) dtype=float32>, h=<tf.Tensor 'cell_2/cell_2/basic_lstm_cell/mul_2:0' shape=(100, 128) dtype=float32>))
>>> h_0
(LSTMStateTuple(c=<tf.Tensor 'MultiRNNCellZeroState/BasicLSTMCellZeroState/zeros:0' shape=(100, 128) dtype=float32>, h=<tf.Tensor 'MultiRNNCellZeroState/BasicLSTMCellZeroState/zeros_1:0' shape=(100, 128) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'MultiRNNCellZeroState/BasicLSTMCellZeroState_1/zeros:0' shape=(100, 128) dtype=float32>, h=<tf.Tensor 'MultiRNNCellZeroState/BasicLSTMCellZeroState_1/zeros_1:0' shape=(100, 128) dtype=float32>), LSTMStateTuple(c=<tf.Tensor 'MultiRNNCellZeroState/BasicLSTMCellZeroState_2/zeros:0' shape=(100, 128) dtype=float32>, h=<tf.Tensor 'MultiRNNCellZeroState/BasicLSTMCellZeroState_2/zeros_1:0' shape=(100, 128) dtype=float32>))
进一步的，如果翻看源代码的话 看介绍的话可以知道 任何RNNCell都需要完成一个.call()的类方法，其实也就是用来实现RNN时序的单步计算，形如(output, next_state) = .call(input, state)；所以说 这就和常见的NN里面的 按照层的前向传播不太一样了，毕竟我们要做的还是进行时序上的传播，而正常的层之间的前向传播 还是照常；进而说在RNN的使用时候，我们需要进行调用call方法；具体的来说 初始输入状态为x_1，而设置的初始隐层状态为h_0，那么就有着(output_1,h_1)=cell.call(x_1,h_0)完成一次时序上的前进，同样的 使用x_2和h_1,我们可以计算出来RNNCell；
这里我们先捋一下整个流程：一方面我们往往使用batch的形式输入数据，于是输入有着(batch_size,input_size)，调用call方法输出两种数据：一种是隐层状态有着(batch_size,state_size) 另外的就是输出(batch_size,output_size);「尽管这样的写法 不需要像在dynamic_rnn里面对于输入进行变形成为[batch_size,max_times,output_size]，但同样的你需要手动的来进行具体次数的call方法，来对应时序单元个数」
怎么说呢，输入一个单词 那么一个时序单元就够，但输入是一个句子 那么这个句子就被反复循环 主要针对其中各个单词来进行的循环「每循环一次换个单词 内部操作应该就是这样」 这也就是时序或者说顺序；参考最上面的第二个图 就是那种感觉；如果是1 VS N，那么就是连输入都不用变，每次循环一次 得到一个输出
这里顺带扯一句 假如我们直接使用之前的 也就是单层的RNN里面的h_0作为初始隐状态信息输入，就会出现TypeError: 'Tensor' object is not iterable.的错误提示，翻看源代码里面的zero_state函数的介绍可以知道，最后实现return _zero_state_tensors(state_size, batch_size, dtype) 是需要调用当前model也就是RNN的隐状态情况的，也就是说初始的h_0其实还是一一对应的，毕竟state_size都是不一样的；「毕竟你三层 本质上只是本身的循环，那么肯定需要基于三层来设置初值」
虽然RNN里面有着输出，毕竟神经网络嘛 哪能离得开输出的情况呢。但也能感觉到在RNN里面 其实对于隐状态情况更为关注，翻开BasicRNNCell和BasicLSTMCell的call函数如下，前者参考上面的RNN的结构图来理解，在BasicRNNCell里面其实output和隐状态的值是一样的，不过定义发生了一波转换，才有上图中当前单元的输出y；所以在BasicRNNCell里面state_size和output_size是一样的；
对于后者的BasicLSTMCell来说，依照标准的(output, next_state) = call(input, state)我们可以看到，位于前者的为output，输出的也正是LSTM里面单纯的h，而LSTM输出的隐状态就包含了h和c两部分，可以看到，其实两者的组合得到的结果；
def call(self, inputs, state):
#... 前略
output = self._activation(self._linear([inputs, state]))
return output, output
def call(self, inputs, state):
new_c = (
c * sigmoid(f + self._forget_bias) + sigmoid(i) * self._activation(j))
new_h = self._activation(new_c) * sigmoid(o)
if self._state_is_tuple:
new_state = LSTMStateTuple(new_c, new_h)
else:
new_state = array_ops.concat([new_c, new_h], 1)
return new_h, new_state
综上可以说 其实RNN里面的output_size其实也都是根据state_size来的，同样的，输出的output部分 其实和隐状态是一样的；
顺带多一句嘴的就是 这里合并是使用的tuple(..)的合并；看源代码 在上面的介绍 其实已经看到了 单个的RNNCell来说，我们每次调用call函数，来得到对应的
output和state信息，在之前的实验中 我们初始化的时候input_data=tf.placeholder(tf.float32,shape=(100,64))，这里单纯的是形如(batch_size,input_size)的格式，这里针对的也还是 如：一个句子里面的一个单词；再具体一点 单层RNNCell针对这样一个句子里面的一个单词 其实就是完成了：对于这个单词 根据h0和x1得到x2和h1； 如果我们有着多层的 如上面这个3层的LSTM，依旧是针对一个单词 其实就是最常用的多层网络进行了3次前向，还是这个单词 使用了三层网络取代之前单层的单层网络来拟合关系罢了；同时 如果不再是一个单词 而是一个句子 比如长度为10 ，那么针对这个长度10的句子，我们又需要调用这个三层LSTM 10次，也就是十次call；「待修改」
dynamic_rnn
显然不停的多次调用call方法挺麻烦的，于是就出现了dynamic_rnn直接调用需要次数的call函数；
相比于单纯的使用call方法，这里其实需要对于input进行变形，如下：
- inputs： If time_major == False (default), this must be a Tensor of shape: [batch_size, max_time, …], or a nested tuple of such elements. If time_major == True, this must be a Tensor of shape:[max_time, batch_size, …], or a nested tuple of such elements. 如果是time_major=True，input的维度是[max_time, batch_size, input_size]，反之就是[batch_size, max_time, input_zise]；
就像上面所说，这里的dynamic_rnn直接进行了需要调用的call函数的次数，而这个次数的体现，其实也就是时序或者说序列本身的长度。考虑到此，其实可以分为固定序列的长度和非固定长度的序列的，如果是前者 序列都是一样的长度 max_time 其实也就是序列本身的长度，反之在非固定长度 这里的max_times其实更多的还是起到了限制的作用：即限制最长进行的循环次数；在从前的实验中 我们初始化的时候input_data=tf.placeholder(tf.float32,shape=(100,64))，这里单纯的是形如(batch_size,input_size)的格式，其实更多的也还是针对的是「单词」 这个级别的问题，如果我们考虑序列长度 其实也就变成了到句子级别的问题了；「毕竟序列嘛，同样 现在的batch 也开始指的是句子的个数了吧 从原有的「单词数目，单词的矩阵」变为了「句子的个数，句子的长度，单词的矩阵」」「可以参考这几个网站来理解tf.nn.dynamic_rnn的输出outputs和state含义和tensorflow高阶教程:tf.dynamic_rnn」
经过dynamic_rnn，返回值有两个：output和state，之前也提到过 其输入的input形式相比于单纯的(batch_size,input_size)多了一个max_time的量的考虑，顾名思义 其实也就是对应的句子里面最长句子的单词数目，就像上面所说 其实也是为了效率考虑 从单词变成了句子；
输出的两者：
- outputs. outputs是一个tensor
- 如果time_major==True，outputs形状为 [max_time, batch_size, cell.output_size ]（要求rnn输入与rnn输出形状保持一致）
- 如果time_major==False（默认），outputs形状为 [ batch_size, max_time, cell.output_size ]
- state. state是一个tensor。state是最终的状态，也就是序列中最后一个cell输出的状态。一般情况下state的形状为 [batch_size, cell.output_size ]，但当输入的cell为BasicLSTMCell时，state的形状为[2，batch_size, cell.output_size ]，其中2也对应着LSTM中的cell state和hidden state
可以看到借助于 tf.nn.dynamic_rnn直接输出运行最终的输出还有状态情况，进而也就完成了前向传播过程；
如下一个简单的示范代码 来体现一波其使用：
import tensorflow as tf
import numpy as np
def dynamic_rnn(rnn_type='lstm'):
# 创建输入数据,3代表batch size,6代表输入序列的最大步长(max time),4代表每个序列的维度
X = np.random.randn(3, 6, 4)
# 第二个输入的实际长度为4
X[1, 4:] = 0
#记录三个输入的实际步长
X_lengths = [6, 4, 6]
rnn_hidden_size = 5
if rnn_type == 'lstm':
cell = tf.contrib.rnn.BasicLSTMCell(num_units=rnn_hidden_size, state_is_tuple=True)
else:
cell = tf.contrib.rnn.GRUCell(num_units=rnn_hidden_size)
outputs, last_states = tf.nn.dynamic_rnn(
cell=cell,
dtype=tf.float64,
sequence_length=X_lengths,
inputs=X)
with tf.Session() as session:
session.run(tf.global_variables_initializer())
o1, s1 = session.run([outputs, last_states])
print(np.shape(o1))
print(o1)
print(np.shape(s1))
print(s1)
if __name__ == '__main__':
dynamic_rnn(rnn_type='lstm')
cell类型为LSTM，我们看看输出是什么样子，如下图所示，输入的形状为 [ 3, 6, 4 ]，经过tf.nn.dynamic_rnn后outputs的形状为 [ 3, 6, 5 ]；「三个数分别代表了batch_size,max_times state_size」state形状为 [ 2, 3, 5 ]，包含了两部分 所以第一个数才是2，其中state第一部分为c，代表cell state;第二部分为h，代表hidden state。可以看到hidden state 与 对应的outputs的最后一行是相等的。另外需要注意的是输入一共有三个序列，但第二个序列的长度只有4，可以看到outputs中对应的两行值都为0，所以hidden state对应的是最后一个不为0的部分。tf.nn.dynamic_rnn通过设置sequence_length来实现这一逻辑。
(3, 6, 5)
[[[ 0.0146346 -0.04717453 -0.06930042 -0.06065602 0.02456717]
[-0.05580321 0.08770171 -0.04574306 -0.01652854 -0.04319528]
[ 0.09087799 0.03535907 -0.06974291 -0.03757408 -0.15553619]
[ 0.10003044 0.10654698 0.21004055 0.13792148 -0.05587583]
[ 0.13547596 -0.014292 -0.0211154 -0.10857875 0.04461256]
[ 0.00417564 -0.01985144 0.00050634 -0.13238986 0.14323784]]
[[ 0.04893576 0.14289175 0.17957205 0.09093887 -0.0507192 ]
[ 0.17696126 0.09929577 0.21185635 0.20386451 0.11664373]
[ 0.15658667 0.03952745 -0.03425637 0.00773833 -0.03546742]
[-0.14002582 -0.18578786 -0.08373584 -0.25964601 0.04090167]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. ]]
[[ 0.18564152 0.01531695 0.13752453 0.17188506 0.19555427]
[ 0.13703949 0.14272294 0.21313036 0.07417354 0.0477547 ]
[ 0.23021792 0.04455495 0.10204565 0.17159792 0.34148467]
[ 0.0386402 0.0387848 0.02134559 0.00110381 0.08414687]
[ 0.01386241 -0.02629686 -0.0733538 -0.03194245 0.13606553]
[ 0.01859433 -0.00585316 -0.04007138 0.03811594 0.21708331]]]
(2, 3, 5)
LSTMStateTuple(c=array([[ 0.00909146, -0.03747076, 0.0008946 , -0.23459786, 0.29565899],
[-0.18409266, -0.30463044, -0.28033809, -0.49032542, 0.12597639],
[ 0.04494702, -0.01359631, -0.06706629, 0.06766361, 0.40794032]]), h=array([[ 0.00417564, -0.01985144, 0.00050634, -0.13238986, 0.14323784],
[-0.14002582, -0.18578786, -0.08373584, -0.25964601, 0.04090167],
[ 0.01859433, -0.00585316, -0.04007138, 0.03811594, 0.21708331]]))
cell类型为GRU，我们看看输出是什么样子，如下图所示，输入的形状为 [ 3, 6, 4 ]，经过tf.nn.dynamic_rnn后outputs的形状为 [ 3, 6, 5 ]，state形状为 [ 3, 5 ]。可以看到 state 与 对应的outputs的最后一行是相等的。
(3, 6, 5)
[[[-0.05190962 -0.13519617 0.02045928 -0.0821183 0.28337528]
[ 0.0201574 0.03779418 -0.05092804 0.02958051 0.12232347]
[ 0.14884441 -0.26075898 0.1821795 -0.03454954 0.18424161]
[-0.13854156 -0.26565378 0.09567164 -0.03960079 0.14000589]
[-0.2605973 -0.39901657 0.12495693 -0.19295695 0.52423598]
[-0.21596414 -0.63051687 0.20837501 -0.31775378 0.77519457]]
[[-0.1979659 -0.30253523 0.0248779 -0.17981144 0.41815343]
[ 0.34481129 -0.05256187 0.1643036 0.00739746 0.27384158]
[ 0.49703664 0.22241165 0.27344766 0.00093435 0.09854949]
[ 0.23312444 0.156997 0.25482553 0.0138156 -0.02302272]
[ 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. ]]
[[-0.06401732 0.08605342 -0.03936866 -0.02287695 0.16947652]
[-0.1775206 -0.2801672 -0.0387468 -0.20264583 0.58125297]
[ 0.39408762 -0.44066425 0.25826641 -0.18851604 0.36172166]
[ 0.0536013 -0.29902928 0.08891931 -0.03930039 0.0743423 ]
[ 0.02304702 -0.0612499 0.09113458 -0.05169013 0.29876455]
[-0.06711324 0.014125 -0.05856332 -0.05632359 -0.00390189]]]
(3, 5)
[[-0.21596414 -0.63051687 0.20837501 -0.31775378 0.77519457]
[ 0.23312444 0.156997 0.25482553 0.0138156 -0.02302272]
[-0.06711324 0.014125 -0.05856332 -0.05632359 -0.00390189]]
此外tf.nn.dynamic_rnn一个新的参数「好吧 只是之前没注意的缘故」。之前我们就说过 对于tf.nn.dynamic_rnn来说，其中的输入相比于常用的[batch_size,input_size]会多一种参数 max_time也就是序列可能的最长长度，在之前的介绍中也说过有关RNN其中层数和时序的关系，可以知道这里的 max_time其实也就是时序的最长长度，如果都是一样的长度，那么这里的 max_time其实也就能代指的是针对这个时序长度所要进行的call操作次数。但同样的 也存在不是一样长度的，那么这里的 max_time更多的只是一种最多次数的限制，实际的设置针对不同长度序列的句子需要进行的call操作的具体词是 使用的就是这里的sequence_length参数
可以参考这个博客 来对于其中的一些变化来进行理解
